1. 摘要

DeepSeek-V3，是一个Mixture-of-Experts（MoE）结构的大语言模型，参数量671B，其中每个token激活的参数量为37B。DeepSeek-V3主要采用Multi-head Latent Attention（MLA）和DeepSeekMoE结构，此外为了expert负载均衡引入了auxiliary-loss-free策略，为了更强的模型性能采用了multi-token prediction（MTP）训练策略。DeepSeek-V3预训练预料一共14.8T个token，并采用SFT和RL进一步对齐增强模型性能。DeepSeek-V3完整的训练一共仅需要2.788M H800 GPU hours。项目链接：DeepSeek-V3

2. DeepSeek-V3模型结构

2.1 Basic Architecture

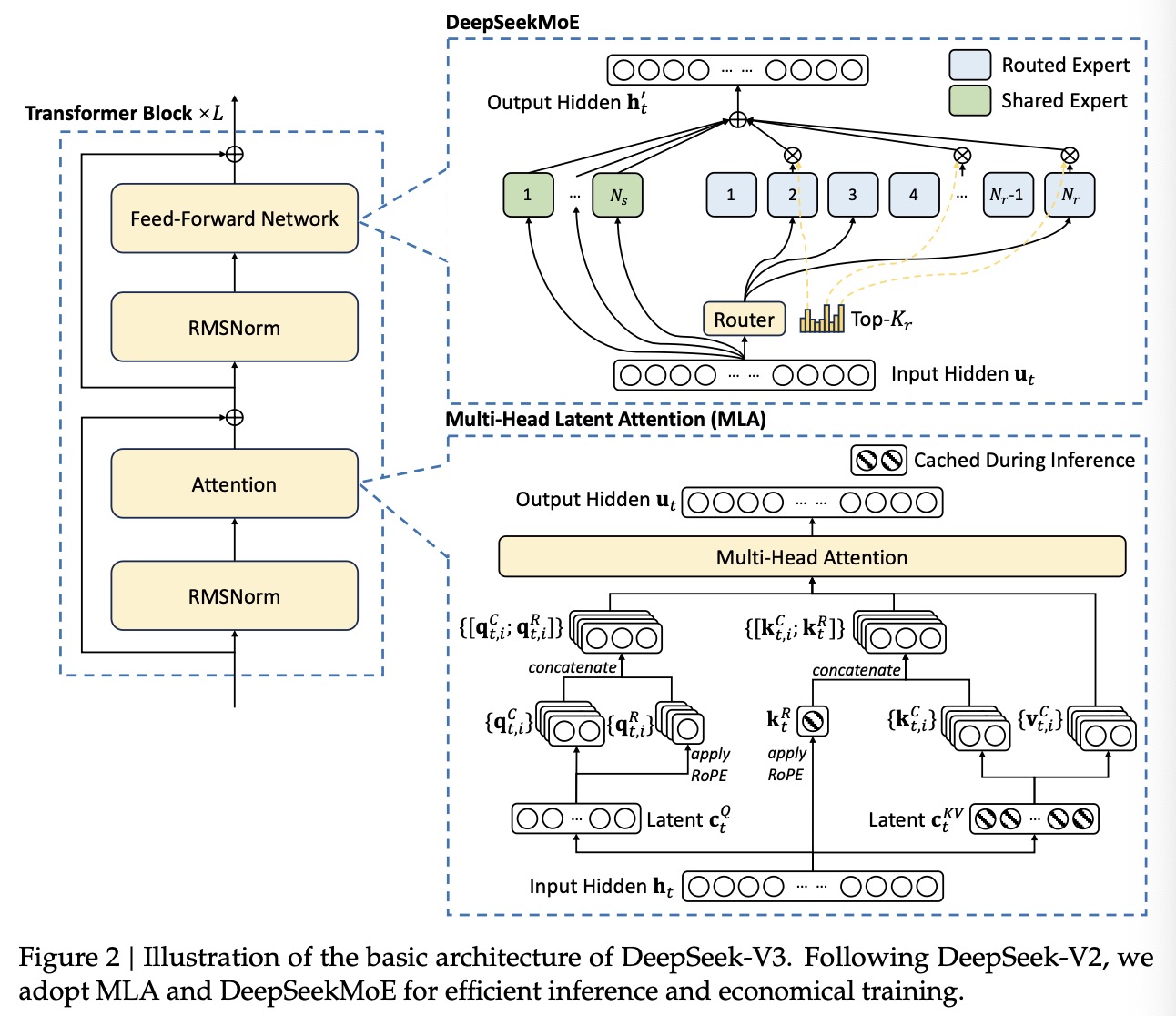
deepseek-v3-architecture

图1: DeepSeek-V3基础结构图

DeepSeek-V3基本结构基于Transformer模型，为了高效推理并降低训练成本，DeepSeek-V3采用了DeepSeek-V2中的MLA和DeepSeekMoE结构。并给予DeepSeek-V2，团队添加了一个auxiliary-loss-free的专家负载均衡策略。图1为MLA和DeepSeekMoE的结构示意图。

2.1.1 Multi-Head Latent Attention

定义$d$为词嵌入向量维度，$n_h$为注意力头数目，$d_h$为每个注意力头的维度，$\bold{h}_t\in\mathbb R^d$表示给定注意力层的第$t$个token的注意力输入向量。MLA的关键在于在推理阶段使用low-rank joint compression技术来减少KV-Cache所占用的存储量：

$$ \textcolor{blue}{\bold{c}_t^{KV}}=W^{DKV}\bold{h}_t,\\ $$
$$ \left[\mathbf{k}_{t,1}; \mathbf{k}^C_{t,2}; \dots; \mathbf{k}^C_{t,n_h} \right] = \mathbf{k}^C_t = W^{UK} \mathbf{c}^{KV}_t, $$
$$ \textcolor{blue}{\mathbf{k}^R_t} = \mathrm{RoPE}(W^{KR} \mathbf{h}_t), $$
$$ \mathbf{k}_{t,i} = \left[\mathbf{k}^C_{t,i}; \mathbf{k}^R_t \right], $$
$$ \left[\mathbf{v}^C_{t,1}; \mathbf{v}^C_{t,2}; \dots; \mathbf{v}^C_{t,n_h} \right] = \mathbf{v}^C_t = W^{UV} \mathbf{c}^{KV}_t. $$

其中$\bold{c}_t^{KV}\in\mathbb R^{d_c}$代表key和value压缩后的隐藏向量；$d_c(\ll d_n n_h)$表明key和value的压缩维度，$W^{DKV}\in\mathbb R^{d_c\times d}$为下投影矩阵，$W^{UK},W^{UV}\in\mathbb R^{d_hn_h\times d_c}$为key和value的上投影矩阵。$W^{KR}\in\mathbb R^{d_h^R\times d}$用于生成carry RoPE key向量的矩阵。在MLA中，只有标蓝的向量（$\textcolor{blue}{\bold{c}_t^{KV}}$和$\textcolor{blue}{\bold{k}_t^R}$）需要在推理阶段存储（相比Multi-Head Attention的KV-Cache开销小很多）。

对于注意力中的query，团队同样执行low-rank compression，这可以减少训练时的激活缓存的开销：

$$ \begin{align*} \bold c_t^Q &= W^{DQ} \bold h_t, \\ \left[\bold q_{t,1}^{C}; \bold q_{t,2}^{C}; \dots; \bold q_{t,n_h}^{C} \right] &= \bold q_t^C = W^{UQ} \bold c_t^Q, \\ \left[\bold q_{t,1}^{R}; \bold q_{t,2}^{R}; \dots; \bold q_{t,n_h}^{R} \right] &= \bold q_t^R = \text{RoPE}(W^{QR} \bold c_t^Q), \\ \bold q_{t,i} &= \left[\bold q_{t,i}^C; \bold q_{t,i}^R \right], \end{align*} $$

其中$\bold c_t^Q\in\mathbb R^{d_c^\prime}$代表query压缩后的隐藏向量；$d_c^\prime(\ll d_hn_h)$为query压缩向量，$W^{DQ}\in\mathbb R^{d_c^\prime\times d},W^{UQ}\in\mathbb R^{d_hn_h\times d_c^\prime}$分别为query的下投影和上投影矩阵，$W^{QR}\in\mathbb R^{d_h^Rn_h\times d_c^\prime}$用于生成carry RoPE query向量的矩阵。

最终，query($\bold q_{t,i}$)，key($\bold k_{j,i}$)，value($\bold v_{j,i}^C$)被用于计算注意力输出$\bold{u}_t$：

$$ \mathbf{o}_{t,i} = \sum_{j=1}^t \text{Softmax}_j \left( \frac{\mathbf{q}_{t,i}^T \mathbf{k}_{j,i}}{\sqrt{d_h + d_h^R}} \right) \mathbf{v}_{j,i}^C,\\ \mathbf{u}_t = W^O [\mathbf{o}_{t,1}; \mathbf{o}_{t,2}; \ldots; \mathbf{o}_{t,n_h}], $$

其中$W^O\in\mathbb R^{d\times d_hn_h}$表示输出投影矩阵。

常规Multi-Head Attention的参数量计算，$W^K\in\mathbb R^{d_hn_h\times d}$，$W^Q\in\mathbb R^{d_hn_h\times d}$，$W^V\in\mathbb R^{d_hn_h\times d}$，$W^O\in\mathbb R^{d\times d_hn_h}$

$$ \begin{align*} \bold{k}_t&=W^K\bold{h}_t\\ [\bold{k}_{t,1},\bold k_{t,2},\cdots,\bold k_{t,n_h}]&=\bold{k}_t\\ \bold v_t&=W^V\bold h_t\\ [\bold v_{t,1},\bold v_{t,2},\cdots,\bold v_{t,n_h}]&=\bold{v}_t\\ \bold q_t&=W^Q\bold h_t\\ [\bold q_{t,1},\bold q_{t,2},\cdots,\bold q_{t,n_h}]&=\bold q_t\\ \bold o_{t,i}&=\sum_{j=1}^t\text{Softmax}_j(\frac{\bold q_{t,i}^T\bold k_{j,i}}{\sqrt{d_h}})\bold v_{j,i}\\ \bold u_t&=W^O[\bold o_{t,1},\bold o_{t,2},\cdots,\bold o_{t,n_h}] \end{align*} $$

因此对于Multi-Head Attention，一层的总参数量为：

$$ 3\times(d_hn_h\times d + d) + d\times d_hn_h + d_hn_h = 4d_hn_hd+3d + d_hn_h $$

对于Multi-Head Latent Attention，一层的总参数量为（不计算RoPE相关的参数，假设$d_c=d_c^\prime$）：

$$ \begin{align*} &(d_c\times d+d) + 2\times(d_hn_h\times d_c+d_c)+(d_c^\prime\times d+d)+(d_hn_h\times d_c^\prime+d_c^\prime)\\ &=2\times(d_c\times d+d)+3\times(d_hn_h\times d_c+d_c)\\ &=d_c(3d_hn_h+2d)+2d+3d_c \end{align*} $$

忽略bias项，MLA参数量与MHA参数量之比：

$$ \delta=\frac{d_c(3d_hn_h+2d)}{4d_hn_hd}=\frac{3+\frac{2d}{d_hn_h}}{4\frac{d}{d_c}} $$

由于$d_c\ll d_hn_h, d_c\ll d$，所以$\delta\ll 1$。

2.1.2 DeepSeekMoE with Auxiliary-Loss-Free Load Balancing

Basic Architecture of DeepSeekMoE. DeepSeekMoE同时使用了finer-grained experts和shared experts，即部分专家是所有token共享，部分是通过路由决定。令$\bold u_t$表示第$t$个token的FFN层输入向量，通过如下公式计算FFN层的输出向量$\bold h_t^\prime$：

$$ \begin{align*} \mathbf{h}_t' &= \mathbf{u}_t + \sum_{i=1}^{N_s} \text{FFN}_i^{(s)} (\mathbf{u}_t) + \sum_{i=1}^{N_r} g_{i,t} \text{FFN}_i^{(r)} (\mathbf{u}_t),\\ g_{i,t} &= \frac{g_{i,t}'}{\sum_{j=1}^{N_r} g_{j,t}'},\\ g_{i,t}' &= \begin{cases} s_{i,t}, & s_{i,t} \in \text{Topk}(\{s_{j,t}|1 \leq j \leq N_r\}, K_r), \\ 0, & \text{otherwise}, \end{cases}\\ s_{i,t} &= \text{Sigmoid} (\mathbf{u}_t^T e_i), \end{align*} $$

其中$N_s$和$N_r$分别为共享专家数目和路由专家数目，$\text{FFN}_i^{(s)}(\cdot)$和$\text{FFN}_i^{(r)}(\cdot)$分别为第$i$个共享专家网络和第$i$个路由专家网络，$K_r$表示每个token输入会被激活的路由专家数目，$g_{i,t}$表示第$i$个路由专家的门控值，$s_{i,t}$表示每个路由专家对该token的分数，$\bold e_i$为第$i$个路由专家的重心向量。与DeepSeek-V2不同的是，DeepSeek-V3使用sigmoid函数来计算每个路由专家对token的分数，并使用一个归一化处理来得到门控值。

Auxiliary-Loss-Free Load Balancing. 团队为了均衡每个路由专家的负载量，提出了一个无额外损失函数的负载均衡方法，具体来说，为每个路由专家引入一个偏置项$b_i$：

$$ \begin{align*} g_{i,t}' = \begin{cases} s_{i,t}, & s_{i,t} + b_i \in \mathrm{Topk}(\{s_{j,t} + b_j | 1 \leq j \leq N_r\}, K_r), \\ 0, & \text{otherwise.} \end{cases} \end{align*} $$

注意偏置项只用于路由选取时，而不影响最终的门控值。对于具体控制方式，团队在训练过程中，以每个训练step为单位，在每个step结束后，如果当前路由专家过载，则会对该专家的偏置降低$\gamma$，如果欠载，则偏置增加$\gamma$，其中$\gamma$为超参数（bias update speed），通过这种动态调整方式，DeepSeek-V3能在训练中保持每个专家负载均衡。

Complementary Sequence-Wise Auxiliary Loss. 为了防止单个sequence出现极端不均衡的情况，团队还采用了一个balance loss：

$$ \mathcal{L}_{Bal} = \alpha \sum_{i=1}^{N_r} f_i P_i, \\ f_i = \frac{N_r}{K_r T} \sum_{t=1}^T \mathbb 1 (s_{i,t} \in \text{Topk}( \{ s_{j,t} | 1 \leq j \leq N_r \}, K_r ) ), \\ s'_{i,t} = \frac{s_{i,t}}{\sum_{j=1}^{N_r} s_{j,t}}, \\ P_i = \frac{1}{T} \sum_{t=1}^T s'_{i,t}, $$

其中balance factor $\alpha$为超参数，会被赋予一个很小的值。$\mathbb 1(\cdot)$是示性函数，$T$表示一个句子中的token数量，损失$\mathcal L_{Bal}$能够鼓励路由专家在句子层级上负载均衡。对于上面的损失计算过程，具体分析如下（不是很明白这个优化目标为啥能让负载均衡？？）：

$$ \sum_{i=1}^{N_r}P_i=\frac{1}{T}\sum_{t=1}^T\sum_{i=1}^{N_r}\frac{s_{i,t}}{\sum_{j=1}^{N_r}s_{j,t}}=1 $$
$$ \begin{align*} \sum_{i=1}^{N_r}f_i&=\frac{N_r}{K_rT}\sum_{t=1}^{T}\sum_{i=1}^{N_r} 1(s_{i,t} \in \text{Topk}( \{ s_{j,t} | 1 \leq j \leq N_r \}, K_r ) )\\ &=\frac{N_r}{K_rT}\sum_{t=1}^TK_r=N_r \end{align*} $$
$$ \mathcal L_{Bal}=\alpha\sum_{i=1}^{N_r}f_iP_i\in[0,\alpha N_r] $$

No Token-Dropping. 由于良好的专家负载均衡，DeepSeek-V3训练阶段不会丢弃任何tokens，此外团队对推理阶段的负载均衡也采取了相应策略，因此在推理阶段也不会丢弃任何tokens。

2.2 Multi-Token Prediction

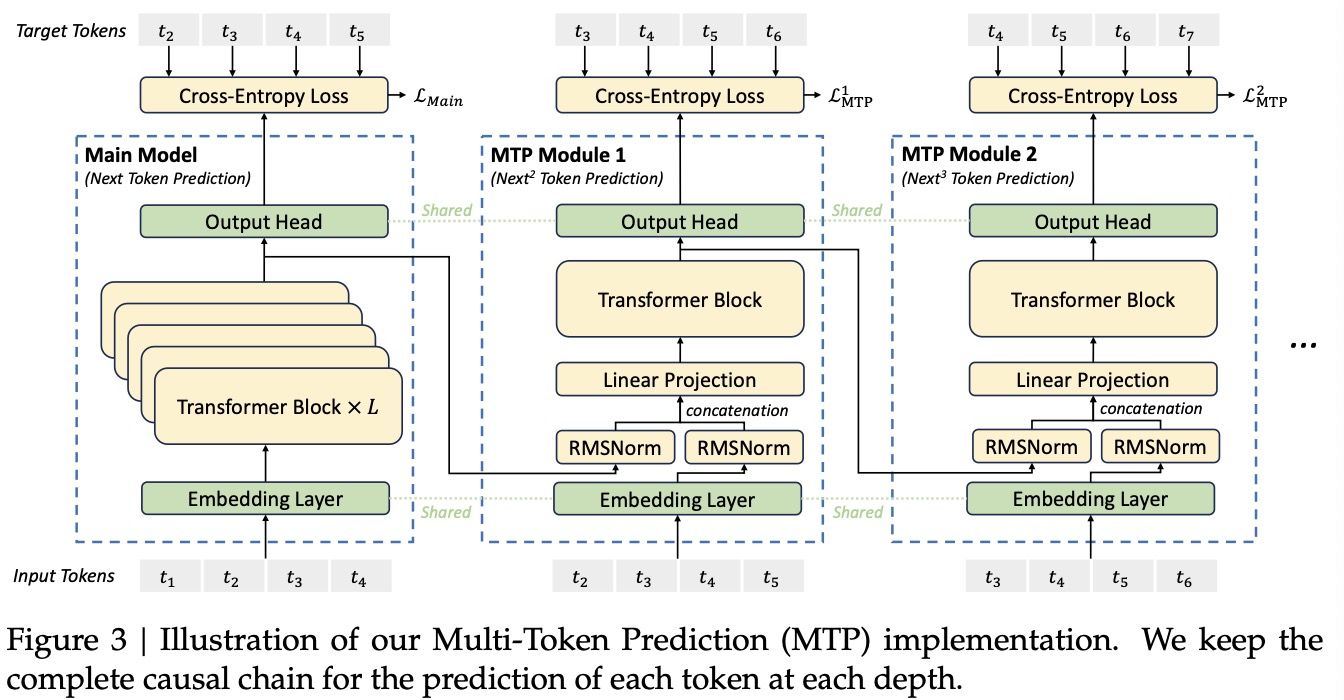
deepseek-v3-mtp

图2: DeepSeek-V3 Multi-Token Prediction结构示意图

DeepSeek-V3中的MTP结构如图2所示，其使用了$D$个MTP模块（不包含主模型）来同时预测额外的$D$个tokens（相当于每个token预测后面1+D个tokens）。其中第$k$（$1\le k\le D$）个MTP模块包含一个与主模型共享的词嵌入向量层$\text{Emb}(\cdot)$，一个与主模型共享的输出头$\text{OutHead}(\cdot)$，一层Transformer块$\text{TRM}_k(\cdot)$，和一个投影矩阵$M_k\in\mathbb R^{d\times 2d}$，对于一个输入序列中的第$i$个输入token $t_i$，对$t_i$的第$k$个预测深度，团队首先结合第$i$个token $t_i$在第$(k-1)$预测深度的Transformer块输出隐藏表征向量 $\bold{h}_i^{k-1}\in\mathbb R^d$ 和第$(i+k)$个token的词嵌入向量$\text{Emb}(t_{i+k})\in\mathbb R^d$，并对结合后的向量进行投影：

$$ \bold{h}_i^{\prime k}=M_k[\text{RMSNorm}(\bold{h}_i^{k-1});\text{RMSNorm}(\text{Emb}(t_{i+k}))], $$

特别的，当$k=1$时，$\bold{h}_i^{k-1}$为主模型输出的表征。结合后的向量$\bold{h}_i^{\prime k}$作为第$i$个token的第$k$预测深度的MTP模块中的Transformer块的输入，并输出第$i$个token在第$k$预测深度的Transformer块输出的隐藏表征向量$\bold{h}_i^k$：

$$ \bold{h}^k_{i}=\text{TRM}_k(\bold{h}_{i}^{\prime k})\quad 1\le i\le T-k, $$

其中$T$代表输入序列的长度，最终，将$\bold{h}_i^k$作为输入，共享输出头计算第$i$个token在第$k$预测深度的预测token的词表维度分布$P_{i+1+k}^k\in\mathbb R^V$，其中$V$为词表大小：

$$ P^k_{i+k+1}=\text{OutHead}(\bold{h}_i^k). $$

经过$\text{OutHead}(\cdot)$后再过一个$\text{Softmax}(\cdot)$得到第$i$个token在第$k$预测深度的预测token的概率分布。

结合图2中的示意图，假设输入序列长度$T=8$，最大额外预测深度$D=4$，即总的MTP结构包含一个主模型和4个MTP块。定义输入序列token为{${t_1,t_2,t_3,t_4,t_5,t_6,t_7,t_8}$}，下面来拆解MTP的损失函数计算过程：

  • 主模型：token {${t_1,t_2,t_3,t_4,t_5,t_6,t_7}$}经过主模型Embedding层和Transformer块输出得到隐藏表征{${\bold{h}_1^0,\bold{h}_2^0,\bold{h}_3^0,\bold{h}_4^0,\bold{h}_5^0,\bold{h}_6^0,\bold{h}_7^0}$}，再经过Output头得到{${P_2^0,P_3^0,P_4^0,P_5^0,P_6^0,P_7^0,P_8^0 }$}，与Target Tokens {${t_2,t_3,t_4,t_5,t_6,t_7,t_8}$}做交叉熵损失得到$\mathcal L_{\text{Main}}$；
  • 第一层MTP模块：输入token {${t_2,t_3,t_4,t_5,t_6,t_7}$}，Transformer块的输入向量为{${\bold{h}_1^{\prime 1},\bold{h}_2^{\prime 1},\bold{h}_3^{\prime 1},\bold{h}_4^{\prime 1},\bold{h}_5^{\prime 1},\bold{h}_6^{\prime 1}, }$}，输出为{${\bold{h}_1^1,\bold{h}_2^1,\bold{h}_3^1,\bold{h}_4^1,\bold{h}_5^1,\bold{h}_6^1 }$}，经过Output头得到{${P_3^1,P_4^1,P_5^1,P_6^1,P_7^1,P_8^1 }$}，与Target Tokens {${t_3,t_4,t_5,t_6,t_7,t_8 }$}做交叉熵损失得到$\mathcal L^1_{\text{MTP}}$；
$$ \bold{h}_i^{\prime 1}=M_1[\text{RMSNorm}(\bold{h}_i^0);\text{RMSNorm}(\text{Emb}(t_{i+1}))]\quad 1\le i\le 6, $$
$$ \bold{h}^1_i=\text{TRM}_1(\bold{h}_i^{\prime 1})\quad 1\le i\le 6, $$
$$ P_{i+2}^1=\text{OutHead}(\bold{h}_i^1)\quad 1\le i\le 6, $$
  • 第二层MTP模块：输入token {${t_3,t_4,t_5,t_6,t_7}$}，Transformer块的输入向量为{${\bold{h}_1^{\prime 2},\bold{h}_2^{\prime 2},\bold{h}_3^{\prime 2},\bold{h}_4^{\prime 2},\bold{h}_5^{\prime 2} }$}，输出为{${\bold{h}_1^2,\bold{h}_2^2,\bold{h}_3^2,\bold{h}_4^2,\bold{h}_5^2 }$}，经过Output头得到{${P_4^2,P_5^2,P_6^2,P_7^2,P_8^2 }$}，与Target Tokens {${t_4,t_5,t_6,t_7,t_8 }$}做交叉熵损失得到$\mathcal L^2_{\text{MTP}}$；
$$ \bold{h}_i^{\prime 2}=M_2[\text{RMSNorm}(\bold{h}_i^1);\text{RMSNorm}(\text{Emb}(t_{i+2}))]\quad 1\le i\le 5, $$
$$ \bold{h}^2_i=\text{TRM}_2(\bold{h}_i^{\prime 2})\quad 1\le i\le 5, $$
$$ P_{i+3}^2=\text{OutHead}(\bold{h}_i^2)\quad 1\le i\le 5, $$
  • 第三层MTP模块：输入token {${t_4,t_5,t_6,t_7}$}，Transformer块的输入向量为{${\bold{h}_1^{\prime 3},\bold{h}_2^{\prime 3},\bold{h}_3^{\prime 3},\bold{h}_4^{\prime 3} }$}，输出为{${\bold{h}_1^3,\bold{h}_2^3,\bold{h}_3^3,\bold{h}_4^3 }$}，经过Output头得到{${P_5^3,P_6^3,P_7^3,P_8^3 }$}，与Target Tokens {${t_5,t_6,t_7,t_8 }$}做交叉熵损失得到$\mathcal L^3_{\text{MTP}}$；
$$ \bold{h}_i^{\prime 3}=M_3[\text{RMSNorm}(\bold{h}_i^2);\text{RMSNorm}(\text{Emb}(t_{i+3}))]\quad 1\le i\le 4, $$
$$ \bold{h}^3_i=\text{TRM}_3(\bold{h}_i^{\prime 3})\quad 1\le i\le 4, $$
$$ P_{i+4}^3=\text{OutHead}(\bold{h}_i^3)\quad 1\le i\le 4, $$
  • 第四层MTP模块：输入token {${t_5,t_6,t_7}$}，Transformer块的输入向量为{${\bold{h}_1^{\prime 4},\bold{h}_2^{\prime 4},\bold{h}_3^{\prime 4}}$}，输出为{${\bold{h}_1^4,\bold{h}_2^4,\bold{h}_3^4 }$}，经过Output头得到{${P_6^4,P_7^4,P_8^4 }$}，与Target Tokens {${t_6,t_7,t_8 }$}做交叉熵损失得到$\mathcal L^4_{\text{MTP}}$；
$$ \bold{h}_i^{\prime 4}=M_4[\text{RMSNorm}(\bold{h}_i^3);\text{RMSNorm}(\text{Emb}(t_{i+4}))]\quad 1\le i\le 3, $$
$$ \bold{h}^4_i=\text{TRM}_4(\bold{h}_i^{\prime 4})\quad 1\le i\le 3, $$
$$ P_{i+5}^4=\text{OutHead}(\bold{h}_i^4)\quad 1\le i\le 3, $$

综上，总的MTP训练目标函数为每一层预测深度的损失总和：

$$ \mathcal L_{\text{MTP}}^1=\text{CrossEntropy}(P^1_{3:8},t_{3:8})\\ \mathcal L_{\text{MTP}}^2=\text{CrossEntropy}(P^2_{4:8},t_{4:8})\\ \mathcal L_{\text{MTP}}^3=\text{CrossEntropy}(P^3_{5:8},t_{5:8})\\ \mathcal L_{\text{MTP}}^4=\text{CrossEntropy}(P^4_{6:8},t_{6:8}) $$

论文中的写法如下，用了$T+1$应该是对长度为T的句子开头补了eos token，本文的推导过程中的句子长度T就是包含了补token后的结果，特此区别。此外这边的每一层损失都是做了$\frac{1}{T}$的归一化处理，这部分理解按照正常的交叉熵公式应该是用$\frac{1}{T-k}$（按本文的$T$处理方式就是$\frac{1}{T-1-k}$），这里需要看源码。

$$ \mathcal{L}_{\text{MTP}}^k = \text{CrossEntropy}(P_{2+k:T+1}^k, t_{2+k:T+1}) = - \frac{1}{T} \sum_{i=2+k}^{T+1} \log P_i^k[t_i] $$

最后对每一层的MTP损失进行均值处理，其中团队添加了一个权重因子$\lambda$，整体的$\mathcal L_{\text{MTP}}$作为DeepSeek-V3的一个额外训练损失。

$$ \mathcal L_{MTP}=\frac{\lambda}{D}\sum_{k=1}^D\mathcal L_{\text{MTP}}^k $$

对于推理阶段中的MTP：由于MTP策略主要用于提升主模型的性能，因此在推理阶段，可以选择直接丢弃这些MTP模块。

References

[1] DeepSeek-AI. “DeepSeek-V3 Technical Report” arXiv preprint axXiv:2412.19437 (2024).